P1
- 코드 강의록에 올려둠.
테일러 급수 식: $f(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f'''(c)(x - c)^3}{3!} + ...$
복습
-
컴퓨터의 제약
- 정확한 값을 출력 불가. 컴퓨터는 0.1을 정확히 표현 못함.
- 사칙연산만 가능
- 2진수
- 유한 반복 - 무한한 계산을 할수 없어 잘라내야 함. 자름 오차 발생. 시험에선 32비트 기준..이라는데 시험에 비트가 왜 연관이 되는가..?
-
테일러 정리 (Taylor Theorem)
- 잘려나간 오차 전체의 절댓값과 잘려나가는 첫째항의 절대값이 같아지는 어떤 거시기 가 있다.
- $\vert\frac{f'''(c)(x-c)^3}{3!}+...\vert == \vert\frac{f'''(거시기)(x-c)^3}{3!}\vert$
- 근데 왜 c중에 하나만 거시기로 바꾸는가? c==거시기는 아닌 건가?
P2
거시기 예 (진짜 이렇게 쓰심)
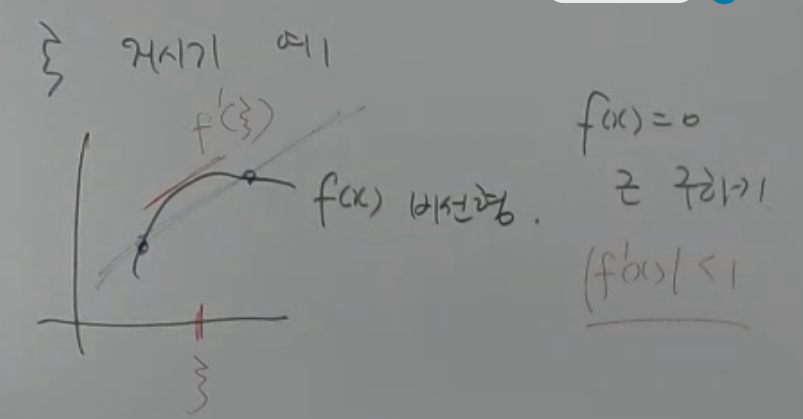
15분 49초
위 그래프에서 $f(x)=0$인 근을 구하고 싶다고 하자.
두 점을 지나는 직선과 기울기가 같은 구간이 딱 봐도 존재할것 같지 않은가.
하지만 그 기울기를 갖는 거시기를 정확히 알 필요가 없다. 저런놈이 당연히 있을것 같다 라는걸 알고있으라는 것.
$\vert f'(x)\vert<1$ 이 구간은 어디다 써먹느냐 하면, 수치해석에서 기울기가 1 보다 작으면 무조건 답을 구할수 있다. 기울기가 1보다 작은 구간을 구하면 된다. 이건 나중에 보여준다고 한다.
테일러 급수와 $e^x$, $sinx$, $cosx$를 한번씩 보여줌. 1번 강의록에 있으니 스킵.
$cosx$를 예로 들어 $x=0.1$일때 각각 3번항 4번항인 $\frac{(0.1)^4}{4!}$ 과 $\frac{-(0.1)^6}{6!}$가 100배 이상 차이난다는 것을 보며 뒤에오는 놈은 허접한 녀석임을 강조.
이로서 알수있는 테일러 Theorem 흐름 - 잘려나가는 오차는 잘려나가는 첫째 항에 좌우됨. 이후 항이 겁내 작아서 영향이 크지 않음.
bjr하면서 안내는 사람들이 많아서 과제 답을 미리 다 설명해줌. 문제푸는 시늉만 해도 만점을 줌.
참고로 x=0일땐 그냥 센터값 그대로 이므로 오차가 없다. 센터에서 벗어나며 생기는 것이 오차다.
P3
오차를 언제 고려하게 되냐면 김정은이 미사일을 쏠때 오차가 중요하다 라고 하심.
과제풀이
28. 약 4.25에서 $\sqrt[4]{4x-1}$ 의 테일러 급수식 두번째 항은?
테일러 급수식 $f(x)=f(c)+f'(c)(x-c)+...$에서 두번째 항 $f'(c)(x-c)$의 센터값 $c=4.25$일 때를 구합니다.
$$f'(x)=\frac{1}{4}(4x-1)^{\frac{1}{4}-1}\cdot4=(4x-1)^{-\frac{3}{4}}$$
$$f'(4.25)=(4*4.25-1)^{-\frac{3}{4}}=(2^4)^{-\frac{3}{4}}=\frac{1}{8}$$
따라서 답은 $\frac{1}{8}(x-4.25)$
34. 함수 $3x^2-7+cosx$ 의 테일러 급수식에서 $x^2$ 의 계수는 몇인가? (함수는 $x$ 의 거듭제곱으로 전개한다)
센터값이 없으니 $c=0$으로 간주합니다.
1강때 센터값을 안잡아주면 나쁜사람이라고 하였으니 킨케이드는 나쁜사람임이 증명되었다.
주어진 함수와 테일러 급수식에서 구해야되는 $x$의 계수가 똑같은데, 이런경우 함수 전체를 미분해서 푸는것도 가능하나 사서 고생하는 셈이 됩니다.
대신 $cos(x)$에서 테일러 급수 식이 $cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ...$ 임을 이용합니다.
이미 함수에서 $x^2$의 계수가 3이 주어졌고, $cosx$의 테일러 급수식에서 $x^2$의 계수가 $-\frac{1}{2!}$이므로
$$3-\frac{1}{2!}=\frac{5}{2}$$
답은 $\frac{5}{2}$ 입니다.
도저히 이해가 안가서 울프람 알파를 돌려본 결과도 동일합니다. $$-6 + \frac{5 x^2}{2} + \frac{x^4}{24} - \frac{x^6}{720} + \frac{x^8}{40320} + O(x^9)$$
여기서 교수님께 여쭙고 싶은게 있습니다. 이 결과를 볼 때, 비선형식을 선형식으로 유도할수 있게 해주는 테일러 급수식에 애초에 비선형식이 아닌 $3x^2$을 넣게 되면 어차피 선형식인 자기 자신 $3x^2$이 나오기 때문에 굳이 계산할 필요가 없는 것으로 이해하는 것이 맞습니까?
P4
35. 약 $\frac{\pi}{4}$ 에서 함수 $sinx+cosx$ 의 테일러 급수식에서, 0이 아닌 세번째 항을 찾아라.
$c=\frac{\pi}{4}$
$f(x)=sinx+cosx$, $f(\frac{\pi}{4})=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$
$f'(x)=cosx-sinx$, $f'(\frac{\pi}{4})=\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=0$
$f''(x)=-sinx-cosx$, $f''(\frac{\pi}{4})=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}$
$f'''(x)=-cosx+sinx$, $f'''(\frac{\pi}{4})=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=0$
$f''''(x)=sinx+cosx$, $f''''(\frac{\pi}{4})=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$
이때 테일러 급수 식 $$f(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f'''(c)(x - c)^3}{3!} + ...$$ 에 넣어보면
$$f(x)=f(c)+0+\frac{f''(c)(x - c)^2}{2!}+0+\frac{f''''(c)(x-c)^4}{4!}+...$$
여기서 0을 제외한 3번째 $\frac{f''''(c)(x-c)^4}{4!}$에 센터값 대입시
답은 $\frac{\sqrt{2}}{4!}(x-\frac{\pi}{4})^4$ 이 됩니다.
한번에 제출 금지!
중간고사와 기말시험을 둘다 칠때 각각 A5에 별표한것들 적어오고
중간 없이 기말고사만 치게 되면 A4에 적어올것. A5던 A4던 양면으로 사용가능.
종이접어서 A5 라는 드립은 삼가야 한다고 한다.
P5
36. 테일러 정리를 이용할 때, $\vertx\vert<\frac{1}{2}$을 만족하는 $x$ 전체 범위에서 $\vertcosx-(1-\frac{x^2}{2})\vert$가 어떤 값보다 작거나 같다고 확신할 수 있는가?
$\vertx\vert<\frac{1}{2}$ 범위처럼 주어질시 눈치있게 센터값을 중앙값으로 잡습니다. $c=0$
$cosx$에서 테일러 급수식 $$cos(x) = 1 + 0 - \frac{x^2}{2!} + 0 + \frac{x^4}{4!}+ ...$$ 에서 자를때 문제에 나온 $\frac{x^2}{2}$ 의 다음항 $0x^3$부터 자르지 말고 한항 더 뒤, $x^4$부터 잘라야 더 정확합니다.
테일러 정리에 따르면 잘려나가는 첫항의 절댓값 $\vert\frac{f''''(0)(x-0)^4}{4!}\vert$ 이 잘려나가는 전체의 값과 같은 거시기가 있습니다.
여기서 $\vertab최댓값\vert\leq\verta최댓값\vert\vertb최댓값\vert$ 임을 이용하여
$$\vert\frac{f''''(0)(x-0)^4}{4!}\vert<\frac{\vert f''''(거시기)최대\vert\cdot\vert(x-0)^4 최대\vert}{4!}$$ ($x$ 범위가 $\leq $가 아니라 $<$로 주어졌으므로 최댓값에서도 똑같이 적용)
이때 $f''''(x)=\vertcosx\vert\leq1$으로 아무리 커봐야 절댓값이 1로 최대 1이 될 수 있고, $x=\frac{1}{2}$일 때 $\vert(x-0)^4 \vert$ 도 최대값 $(\frac{1}{2})^4$를 갖습니다.
따라서 답은 $\frac{1*(\frac{1}{2})^4}{4!}$ 입니다.
- 진도는 노트기준으로 진행하나 순서가 맞다는 보장이 없음.
P6
Nested multiplification (노트에서 찾을것)
$$y=a_3x^3+a_2x^2+a_1x+a_0=a_0+x(a_1+x(a_2+x(a_3)))$$
총 3번 곱셈. 컴퓨터로 풀기 쉬워진다. TIS-100에서도 곱셈만 나오면 고통 받던 것 생각하면 왜 쉬워지는지 이해가 쉽다.
프로그램 짜는 법은 시험에 안나온다는데 diffExam2017~2020.c파일로 코드시험이 나온다고 얘기하셨다. 뭐가 맞는건지 모르겠다.
P7
페이지 한번 변경. 출석코드 적음
칼같이 적으란 얘기가 아니라 성의를 표하라는것. 그게 어떤건지 난 아직 감이 안온다. 이론? 구조? 방식?
27. 다항식 $p(x)=6(x+3)+9(x+3)^5-5(x+3)^8-(x+3)^{11}$ 이 어떤 방법을 쓰면 컴퓨터로 효과적으로 풀수 있는지 설명하라.
왕 X를 $X=x+3$ 으로 잡을 때
$P(X-3)=6X+9X^5-5X^8-X^{11}$ $=X(6+9X^4-5X^7-X^{10})$ $=X(6+X^4(9-5X^3-X^6))$ $=X(6+X^4(9+X^3(-5-X^3)))$
이렇게 Nested multiplication 형태로 전개하면 더 효과적으로 컴퓨터에서 해결할 수 있습니다.
$X^4=pow(X,4)$ 로 하면 회사에서 모가지 잘림.
반올림 / 무조건 자름 (Rounding / chopping) - 올려둔 족보에서 한번 찾아볼 것.
round 와 floor의 차이라고 보면 될것 같기도 하다.
| 방법 | 숫자 | 오차 | 결과 |
|---|---|---|---|
| 반올림 | 0.150...0 | 0.05=$\frac{1}{2}\cdot0.1$(소수점 이하 한자리) | 0.2 |
| 소숫점이하 1자리남기고 | 0.20...0 | 0.0 | 0.2 |
| 방법 | 숫자 | 오차 | 결과 |
|---|---|---|---|
| 무조건자름(chopping) | 0.10...0 | 0.0 | 0.1 |
| 소숫점이하 1자리남기고 | 0.19...9 | 0.09...9 $\cong $ 1 | 0.1 |
소수점 이하 n자리 남기고 반올림 오차 $\leq\frac{1}{2}*10^{-n}$
소수점 이하 n자리 남기고 chopping 오차 $<10^{-n}$
책이 자주바뀌는 이유: 안바뀌면 니들이 안사니까. 그래서 교수님은 책을 잘 안바꾼다고 함.
P8
30. $(1+x)^n$의 테일러 급수는 binomial theorem 으로도 알려져 있다. 해당 정리는 $x^2<1$에서 $(1+x)^n=1+nx+\frac{n(n-1)}{2!}x^2+\frac{n(n-1)(n-2)}{3!}x^3+...$ 임을 보인다. 해당 함수의 테일러 급수 식을 유도하고 각각 $n=2, n=3, n=\frac{1}{2}$ 에서 그 형태를 보이라. 그다음 $n=\frac{1}{2}$의 형태를 이용하여 $\sqrt{1.0001}$ 을 소숫점 이하 15자리 정밀도로 반올림하여 나타내라.
$x^2<1$ → $-1<x<1$ → 센터값은 $c=0$
$f(c)=(1+c)^n=1$
$f'(c)=n(1+c)^{n-1}=n$
$f''(c)=n(n-1)(1+c)^{n-2}=n(n-1)$
이를 테일러 급수식 $f(x)=f(c)+f'(c)(x-c)+...$에 넣을시
$c=0$에서 $f(c)=1$, $f'(c)=n$, $f''(c)=n(n-1)$
$$f(x)=(1+x)^n=1+n(x-0)+\frac{n(n-1)}{2!}(x-0)^2+\frac{n(n-1)(n-2)}{3!}(x-0)^3+...$$ $$=1+nx+\frac{n(n-1)}{2!}x^2+\frac{n(n-1)(n-2)}{3!}x^3+...$$ 이 유도됩니다.
- $n=2$일때
$$(1+x)^2=1+2(x-0)+\frac{2(2-1)}{2!}(x-0)^2+\frac{2(2-1)(2-2)}{3!}(x-0)^3...$$
$$=1+2x+x^2$$
- $n=3$일때
$$(1+x)^3=1+3x+\frac{3(3-1)}{2!}x^2+\frac{3(3-1)(3-2)}{3!}x^3+\frac{3(3-1)(3-2)(3-3)}{4!}x^4...$$ $$=1+3x+3x^2+x^3$$
P9
- $n=\frac{1}{2}$ 일때
$$(1+x)^{\frac{1}{2}}=1+\frac{1}{2}x+\frac{\frac{1}{2}(\frac{1}{2}-1)}{2!}x^2+\frac{\frac{1}{2}(\frac{1}{2}-1)(\frac{1}{2}-2)}{3!}x^3+...$$ $$=1+\frac{1}{2}x+\frac{-\frac{1}{4}}{2!}x^2+\frac{\frac{3}{8}}{3!}x^3+...$$ $$=1+\frac{1}{2}x-\frac{x^2}{2^2\cdot2!}+\frac{3x^3}{2^3\cdot3!}+...$$
- 마지막 식을 이용한 $\sqrt{1.0001}$ 소수점 이하 14자리까지
교수님께선 decimal point를 10진수로 15자리까지이므로 소수점 이하 14자리까지라고 하셨지만, decimal point의 사전적 정의는 소수점이기에 번역하면 소수점 15자리까지가 되는데, 어느것이 맞는지 모르겠다.
소수점 이하 14자리까지 정확하려면 오차는 $\frac{1}{2}*10^{-14}$미만이여야 합니다.
P10
-14를 -4로 오타치고 시작, 유의할것.
$n=\frac{1}{2}$ 일때 유도한 식을 이용해 $\sqrt{1.0001}=(1+x)^{\frac{1}{2}}$ 로 생각할때 $x=10^{-4}$ 가 됩니다.
잘려나가는 첫째 항을 유도한 식 4번째 항으로 정하면 $x^3=(10^{-4})^3=10^{-12}$ 가 되어 오차가 12자리로 너무 큽니다.
따라서 잘려나가는 오차가 요구되는 정확도보다 작은 5번째 항부터 자르면 $10^{-16}$ 으로 문제의 요구사항을 만족할 수 있습니다.
이전에 유도한 식을 5번째 항까지 계산하진 않았으므로 이어서 계산을 해보면
$$=\frac{\frac{1}{2}(\frac{1}{2}-1)(\frac{1}{2}-2)(\frac{1}{2}-3)}{4!}(x-0)^4=\frac{(-1)(-3)(-5)}{4^2\cdot4!}x^4$$ 가 됩니다.
32. 30번을 이용하여 $(1+x^2)^{-1}$ 의 급수식을 구하라.
유도한 식 $$(1+x)^n=1+nx+\frac{n(n-1)}{2!}x^2+\frac{n(n-1)(n-2)}{3!}x^3+...$$ 에 $n$ 대신 -1을 넣고 $x$ 대신 $x^2$ 를 넣습니다.
$$= 1+(-1)x^2+\frac{(-1)(-1-1)(x^2)^2}{2!}+\frac{(-1)(-1-1)(-1-2)(x^2)^3}{3!}+...$$
$$=1-x^2+\frac{x^4}{2!}-\frac{6x^6}{3!}+...$$
HW1 풀이 끝, 31분 37초부터 마저 볼것.
미분시 0이나오는 경우.. 뭐 하라고? x 대신 x^2를 넣으라는건 이미 미분된 결과식에 그냥 x^2를 넣으라는거지 처음부터 x^2넣고 다시계산하라는건 아님.
x = 진짜답, x* = 컴계산 답/결과 절대 오차는 \vertx - x*\vert
상대오차는 \vert\frac{x-x*}{x}\vert ~= \vert\frac{x-x*}{x*}\vert <- x 모를때 위 상대오차는 그냥 약속같은것으로 외워라.
x를 모를때도 있다. \vertx-x*\vert가 답이 존재하는 공간임.
P11
테일러 급수 변형
늙을수록 중요한거만 얘기하고 구질구질한건 얘기 안하는 경향이 생긴다고 함.
테일러 급수식 삽입
x=c+h c: 센터, 관심범위 h: 엄청작은값. 경험상 \vertx\vert*10^-3
x=c+h로 대체.
f(c+h)=f(c)+f'(c)(c+h-c)+... 이 c를 x로 바꿔 앞 x와 다른 센터개념으로 생각
f(x+h) = f(x) + f'(x)h + \frac{f''(x)h^2}{2!}+... f''(x)값도 모르기때문에 3번항부터 잘라냄.
f'(x) = \frac{f(x+h)-f(x)}{h} + (\frac{-f''(x)h}{2!}+...) f'(x) = \frac{f(x+h)-f(x)}{h} + 오차 O(h)
이때 오차크기 O(n)은 당연히 h에 비례.