수치해석 메모 1
추천 편집사이트 참조
마크다운 윗첨자 아래첨자 수식 ^ str ^ 및 ~ str ~이 안될시 <sup> <sub> 사용
P1
수치해석의 정의
컴을 이용하되 컴의 제약을 고려하면서 해석학 문제 풀기.
시험
학교 지침 따름
| 시험 방식 | 비고 |
|---|---|
| 온라인 | 오픈북/인터넷, 채팅금지 |
| 대면 | A4용지에 적어와서 사용가능 |
학점
학교 지침 따름
교재
Kincaid 책 6판, Numercial Mathematics and computing
과제
9개
- 프로그램 1, 프로그램 과제는 답 코드를 사전에 알려줌. 교수는 C 언어 사용(WHY???)
- 일반 8
P2
테일러 급수
컴퓨터는 사칙연산밖에 안되서 $y=ax^3+bx^2+cx+d$ 와 같은 다항식만 풀수있음.
하지만 비선형식인 $e^x$, $sin(x)$, $cos(x)$ 는 풀수가 없음.
따라서 컴퓨터로 풀수있게 $f(x)$를 center C에서 다항식으로 흉내낸 것이 바로 테일러 급수 라 칸다.
$$★ f(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f'''(c)(x - c)^3}{3!} + ...$$
Center에서 많이 떨어지면 아래처럼 오류가 커져 쓸 수 없게 된다. 망한다고 보라고 하심.

테일러 급수는 $x=c$에서 n번 미분한 결과가 서로 값이 동일하도록 만들어 둠.
$$\lim\limits_{x=c}f'(x) = f'(c)(1-0) + 0 + 0 + ... = f'(c)$$
P3
테일러 급수 연습 - $e^x$
테일러 급수 식: $f(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f'''(c)(x - c)^3}{3!} + ...$
Center C는 직접 정함. 아무데서나 흉내내라고 하면 말이 안되니 따로 써있지 않으면 $c=0$ 으로 간주. 값을 안잡아 주면 나쁜 사람이라는 데 본인은(는) 이 결정을 기억할 것입니다.
- $e^x$ 의 미분값은 자기자신이다. 어디서 군머티내며 잊어먹은거 자랑하지 말자.
$f(x) = e^x$ 에 $c = 0$
$f'(x)=f''(x)=f'''(x)= e^x$ $e^x=e^0+e^0(x-0)+\frac{e^0(x-0)^2}{2!}+\frac{e^0(x-3)^3}{3!}$
$$★ e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...$$
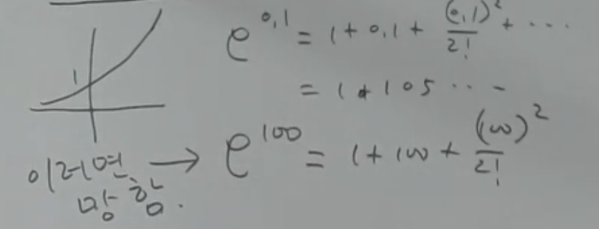
이때 $x=0.1$일때는 쓸만 하지만 $x=100$일때는 망함. 애초 유도센터 0 과 너무 멀리 떨어져있음. 여기서 너무의 기준은 $|x-c|<0.5$로 이걸 초과하면 처형 대상. 시험에는 안나오나 알아는 둘 생각. 시험에서 범위를 학생이 직접 결정할 문제는 없음.
P4
x와 c의 편차가 커질수록 함수에 따라 오차가 얼마나 벌어지는지는 다 다름. 테일러 급수는 자신들이 수용가능한 오차범위 내에서 쓸모가 있는 것.
테일러 급수 연습 - $sinx$
테일러 급수 식: $f(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f'''(c)(x - c)^3}{3!} + ...$
$f(x)=sinx$ $f'(x)=cosx$ $f''(x)=-sinx$ $f'''(x)=-cosx$
$sinx=sin0+cos0(x-0)+\frac{-sinx(x-0)^2}{2!}+\frac{-cosx(x-0)^3}{3!}+...$
$$★ sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!}+...$$
P5
테일러 급수의 효용성
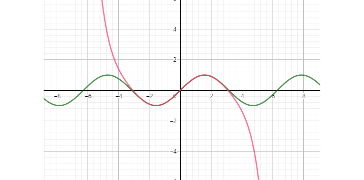
위에 나온 4항까지만의 $sin(x)$ 테일러 급수식으로도 상당히 해당 구간에서 정확한 결과를 보여줌. 위는 지오지브라에 돌린 모습. 놀랍게도(어쩌면 당연하게도) Latex 문법을 이해한다.
테일러 급수 연습 - $cosx$
테일러 급수 식: $f(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f'''(c)(x - c)^3}{3!} + ...$
$f(x)=cosx$ $f'(x)=-sinx$ $f''(x)=-cosx$ $f'''(x)=sinx$
$cosx=cos0+(-sin0)(x-0)+\frac{-cos0(x-0)^2}{2!}+\frac{sin0(x-0)^3}{3!}+...$
$$★ cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ...$$
P6
C반 질문 내용
$sin10$ 계산?
- 센터를 10 가까운 수로 잡음.
- 센터값에서의 $f(c),f'(c),f''(c),...$ 값을 알아야 함.
수치해석 용도 예시
자율주행 카메라
█████████
██████ █
████ ███
██ █████
█████████
이런 아스팔트의 흰 선을 보는 경우
| 0 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 255 | 0 |
| 0 | 0 | 255 | 0 | 0 |
| 0 | 255 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
이런식으로 인식됨.
여기서 테일러급수에 $x-c=h$로 변형한 변형식 $f'(x)=\frac{f(x+h)-f(x)}{h}$로 $h$를 작은 숫자, 해상도로 치면 1로 설정시 $|f'(x)|=|\frac{255-0}{1}| or |\frac{255-255}{1}| or |\frac{0-0}{1}|$ 같은 계산만 하게됨. (음수는 의미없으니 절댓값 씌움)
이미지에 미분계산을 하여 값이 큰값으로 바뀌게 되는 지점을 외곽선으로 판별
테슬라가 오질나게 비싼 라이다 대신 값싼 카메라를 쓰는건 올바른 판단이였다고 본인도 동의.
P7
테일러 급수에서 유한계산
$e^x = 1 + x + \frac{x^2}{2!} + ...$
3번째 항에서 자름 --> 오차발생.
오차 최대 크기?
테일러 Theorem: 테일러 급수에서 잘려나가는 오차 전체크기가 잘려나가는 첫째 항에 좌우됨.
$$f(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f'''(c)(x - c)^3}{3!}$$
써놓은 마지막 항부터 잘라낸다고 할때, 해당 항 포함 잘려나간 전체 합은 잘려나간 첫째항보다 크지 않은 뭔가 거시기한 값이 있다.
$$\frac{f'''(거시기)(x-3)^3}{3!}=이후 나머지 전체 합$$
위 식이 성립하는 거시기가 있는데 그 값을 모른다. 하지만 그 값도 최댓값이 있을것이고, 그 최대값만 따지자는 것. 이 최대값에서의 오차보단 더 커질수는 없다는 것이 테일러 Theorem이라는 것.
최대값 구하는거도 한번에 구하기 힘드니 $f'''(거시기)$ 와 $(x-c)^3$의 최대값을 개별적으로 구해서 구하라는 듯.
x=거시기 대입을 거시기를 박아넣는다는 놀라운 표현을 사용하셨다. 내가치는 드립이 아님.